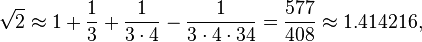จริงหรือไหมชาวฮินดู รู้จักทฤษฎีบทพีทาโกรัสก่อนพีทาโกรัสค้นพบ ทฤษฎีบทพีทาโกรัส

คณิตศาสตร์เวทเป็นแหล่งความรู้แรกและสำคัญที่สุด แบ่งปันอย่างไม่เห็นแก่ตัวโดย ‎ฮินดู ไปทั่วโลก คำถามที่พบบ่อยของชาวฮินดูจะตอบการค้นพบบางอย่างทั่วโลกซึ่งอาจมีอยู่ในศาสนาฮินดูเวท และอย่างที่ฉันเคยพูดเสมอว่า เราจะไม่ตัดสิน เราจะเขียนบทความขึ้นมาเอง คุณควรจะรู้ว่าควรยอมรับหรือปฏิเสธ เราต้องเปิดใจอ่านบทความนี้ อ่านและเรียนรู้เกี่ยวกับประวัติศาสตร์ที่เหลือเชื่อของเรา มันจะทำให้คุณทึ่ง ! ! !

แต่ก่อนอื่น ให้ฉันระบุกฎของชื่อเดียวกันของสติกเลอร์:
“ไม่มีการค้นพบทางวิทยาศาสตร์ใดที่ได้รับการตั้งชื่อตามผู้ค้นพบดั้งเดิม”
ตลกใช่มั้ย
มีการอ้างว่าชาวบาบิโลนรู้จักและใช้กฎของสามเหลี่ยมมุมฉากนานก่อนบาวฮายานาและพีทาโกรัส นอกจากนี้ยังอ้างว่าได้รับการพัฒนาก่อน Euclid และแสดงได้ดีมากใน Euclid's Elements บางคนอ้างว่าเป็นคนจีนที่ค้นพบก่อนใคร

ฉันจะไม่ไปว่าใครเป็นผู้ค้นพบก่อน แต่ฉันจะอธิบายทฤษฎีของ Bauhayana เนื่องจากเว็บไซต์ของเรามีไว้เพื่อรู้เกี่ยวกับศาสนาฮินดู และไม่ใช่เพื่อพิสูจน์ว่าศาสนาฮินดูนั้นยิ่งใหญ่ที่สุดอย่างไร

ดังนั้น Baudhayana (800 ก่อนคริสตศักราช) เป็นผู้เขียนพระสูตร Baudhayana ซึ่งครอบคลุมธรรมะ พิธีกรรมประจำวัน คณิตศาสตร์ ฯลฯ เขาเป็นสมาชิกของโรงเรียน Yajurveda และมีอายุมากกว่า Apastamba ผู้ประพันธ์พระสูตรคนอื่นๆ
เขาเป็นผู้เขียนภาคผนวก Sulba Sutra ที่เก่าแก่ที่สุดใน Vedas ซึ่งให้กฎสำหรับการสร้างแท่นบูชาที่เรียกว่า Baudhayana Sulbasutra สิ่งเหล่านี้มีความโดดเด่นจากมุมมองของคณิตศาสตร์ เนื่องจากมีผลลัพธ์ทางคณิตศาสตร์ที่สำคัญหลายอย่าง รวมทั้งการให้ค่า pi กับความแม่นยำระดับหนึ่ง และการระบุเวอร์ชันของสิ่งที่ปัจจุบันรู้จักกันในชื่อทฤษฎีบทพีทาโกรัส

ลำดับที่เกี่ยวข้องกับไตรลักษณ์ของพีทาโกรัสดั้งเดิมได้รับการตั้งชื่อว่าลำดับ Baudhayana ลำดับเหล่านี้ถูกใช้ในการเข้ารหัสเป็นลำดับสุ่มและสำหรับการสร้างคีย์

ทฤษฎีบทพีทาโกรัส
กำลังสองของด้านตรงข้ามมุมฉากของสามเหลี่ยมมุมฉากเท่ากับผลบวกของกำลังสองของอีกสองด้าน

รัฐพุทธยานา:
“พื้นที่ที่เกิดจากเส้นทแยงมุมของสี่เหลี่ยมผืนผ้าเท่ากับผลรวมของพื้นที่ที่เกิดจากสองด้าน

Baudhayana ระบุทฤษฎีบทพีทาโกรัสไว้ในหนังสือของเขาชื่อ Baudhayana Sulbasutra (800 ก่อนคริสตศักราช) อนึ่ง Baudhayana Sulbasûtra เป็นหนึ่งในหนังสือที่เก่าแก่ที่สุดเกี่ยวกับคณิตศาสตร์ขั้นสูง shloka (ข้อ) ที่เกิดขึ้นจริงใน Baudhayana Sulbasutra ที่อธิบายทฤษฎีบทของ Pythagoras แสดงไว้ด้านล่าง:

ดีรฆะยักษณายา ราชจูห์ ปาร์สวามานี, ติยาทัมมานี,
ชะ ยตปรถากภูเต คุรุสตาดุภยัน กะโรติ.

ที่น่าสนใจคือ Baudhayana ใช้เชือกเป็นตัวอย่างใน shloka ข้างต้น ซึ่งสามารถแปลได้ว่า - เชือกที่ยืดไปตามความยาวของเส้นทแยงมุมทำให้เกิดพื้นที่ซึ่งด้านแนวตั้งและแนวนอนรวมกัน อย่างที่คุณเห็น เห็นได้ชัดว่านี่อาจเป็นวิธีที่ใช้งานง่ายที่สุดในการทำความเข้าใจและแสดงภาพทฤษฎีบทพีทาโกรัส (และเรขาคณิตโดยทั่วไป) และดูเหมือนว่าเบาดายานาจะทำให้กระบวนการเรียนรู้ง่ายขึ้นโดยการสรุปผลทางคณิตศาสตร์ใน shloka ง่ายๆ ในภาษาของคนธรรมดา .

บางคนอาจบอกว่านี่ไม่ใช่ข้อพิสูจน์ทางคณิตศาสตร์ที่แท้จริงของทฤษฎีบทพีทาโกรัส และเป็นไปได้ว่าพีทาโกรัสให้ข้อพิสูจน์ที่ขาดหายไป แต่ถ้าเราดูในซุลบาสุตราฉบับเดียวกัน เราพบว่าการพิสูจน์ทฤษฎีบทพีทาโกรัสนั้นมาจากทั้งบอดฮายานาและอปัสตัมบาในสุลบาสูตร! เพื่อให้ละเอียดยิ่งขึ้น shloka จะแปลว่า -
เส้นทแยงมุมของสี่เหลี่ยมผืนผ้าเกิดจากตัวมันเองทั้งสอง (พื้นที่) แยกจากกันโดยทั้งสองด้าน

ทฤษฎีบทปีทาโกรัสสมัยใหม่
นัยของข้อความข้างต้นนั้นลึกซึ้งเพราะมันแปลโดยตรงเป็นทฤษฎีบทพีทาโกรัส และเห็นได้ชัดว่า Baudhayana พิสูจน์ทฤษฎีบทพีทาโกรัส เนื่องจากการพิสูจน์ในภายหลังส่วนใหญ่มีลักษณะทางเรขาคณิต การพิสูจน์เชิงตัวเลขของ Sulba Sutra จึงถูกละเลยไป แม้ว่า Baudhayana ไม่ใช่นักคณิตศาสตร์ชาวอินเดียเพียงคนเดียวที่ได้ให้หลักฐานและพิสูจน์แฝดสามของ Pythagorean

นอกจากนี้ Apastamba ยังให้ข้อพิสูจน์สำหรับทฤษฎีบทของพีทาโกรัส ซึ่งอีกครั้งเป็นตัวเลขในธรรมชาติ แต่น่าเสียดายอีกครั้งที่การสนับสนุนที่สำคัญนี้ถูกละเลย และพีธากอรัสได้รับการให้เครดิตอย่างผิดๆ โดยซิเซโรและนักคณิตศาสตร์ชาวกรีกยุคแรกสำหรับทฤษฎีบทนี้

นอกจากนี้ Baudhayana ยังนำเสนอการพิสูจน์ทางเรขาคณิตโดยใช้สามเหลี่ยมหน้าจั่ว ดังนั้นเพื่อให้แม่นยำยิ่งขึ้น เราให้การพิสูจน์ทางเรขาคณิตเป็นของ Baudhayana และการพิสูจน์ทางตัวเลข (โดยใช้ทฤษฎีจำนวนและการคำนวณพื้นที่) ให้กับ Apastamba นอกจากนี้ นักคณิตศาสตร์ชาวอินเดียโบราณอีกคนหนึ่งชื่อ Bhaskara ได้ให้ข้อพิสูจน์ทางเรขาคณิตและตัวเลขที่ไม่เหมือนใครในเวลาต่อมา ซึ่งเป็นที่ทราบกันดีอยู่แล้วว่ามันมีลักษณะทั่วไปและใช้ได้กับรูปสามเหลี่ยมทุกประเภท และไม่สอดคล้องกัน (ไม่ใช่แค่หน้าจั่วเหมือนในข้อพิสูจน์เก่าๆ บางข้อ)

วนรอบจัตุรัส

ปัญหาอีกประการหนึ่งที่บัณฑิตายานาแก้ไขก็คือการหาวงกลมที่มีพื้นที่เท่ากับสี่เหลี่ยมจัตุรัส พระสูตร i.58 ของเขาให้การก่อสร้างนี้:

วาดครึ่งเส้นทแยงมุมตรงกลางไปทางเส้นตะวันออก-ตะวันตก จากนั้นอธิบายวงกลมพร้อมกับหนึ่งในสามของส่วนที่อยู่นอกสี่เหลี่ยม

รากที่สองของ 2
Baudhayana i.61-2 (อธิบายเพิ่มเติมใน Apastamba Sulbasūtra i.6) ให้ความยาวของเส้นทแยงมุมของรูปสี่เหลี่ยมจัตุรัสในแง่ของด้าน ซึ่งเทียบเท่ากับสูตรสำหรับรากที่สองของ 2:

สัมมายา ทวิการานี. พราหมณัม ตรีเยนะ วาร์ดาเยต
แทค คาทูร์เธนัตมาคาตุสทริมโซเนนา สาวิเสสาห์

เส้นทแยงมุม [สว่าง “ทวีคูณ”] ของสี่เหลี่ยมจัตุรัส มาตรการจะเพิ่มขึ้นหนึ่งในสามและลดลงหนึ่งในสี่ภายในวันที่ 34 นั่นคือเส้นทแยงมุมโดยประมาณ

เส้นทแยงมุม [สว่าง “ทวีคูณ”] ของสี่เหลี่ยมจัตุรัส มาตรการจะเพิ่มขึ้นหนึ่งในสามและลดลงหนึ่งในสี่ภายในวันที่ 34 นั่นคือเส้นทแยงมุมโดยประมาณ

นั่นคือ,

ซึ่งเป็นทศนิยมห้าตำแหน่งที่ถูกต้อง