ทำไมเราถึงต้องเรียนคณิตศาสตร์ เพื่อเรียนวิทยาศาสตร์?

ทำไมเราถึงต้องเรียนคณิตศาสตร์ เพื่อเรียนวิทยาศาสตร์?

เชื่อว่าเราทุกคนคงจะรู้จักเพื่อนๆ หรือหลานๆ สักคน ที่บอกว่าชอบเรียนวิทยาศาสตร์มาก แต่ไม่ชอบเลขเอาเสียเลย บางคนอาจจะสงสัยว่าแล้วเราจะเรียนคณิตศาสตร์ไปทำไม มีประโยชน์อะไร

วันนี้จะมาลองอธิบายดูจากตัวอย่างที่ "ผิด" ให้ฟัง ว่าหากเราไม่ใช้คณิตศาสตร์ จะเกิดผลร้ายได้เพียงใด

วันนี้เราจะมาพูดถึง "ทฤษฎีโลกแบน" (ซึ่งเป็นทฤษฎีที่ผิด เพราะความจริงแล้วโลกเป็นทรงกลม) และเราจะมาดูกันว่าเพราะเหตุใดทฤษฎีเหล่านี้จึงผิด และคณิตศาสตร์จะสามารถช่วยเราได้อย่างไร

แน่นอนว่า มนุษย์ยุคปัจจุบันแทบไม่มีใครไม่รู้แล้ว ว่าจริงๆ แล้วโลกเป็นทรงกลม แต่เป็นเรื่องที่น่าเศร้าที่ยังมีมนุษย์เป็นจำนวนไม่น้อย ที่พยายามปฏิเสธเรื่องที่แม้กระทั่งชาวกรีกโบราณก็รู้กันเป็นอย่างดีตั้งแต่ยุคกรีกโบราณตั้งแต่เมื่อสองพันกว่าปีที่แล้ว

ส่วนตัวแล้ว บางทีผมก็ติดตาม "ทฤษฎีโลกแบน" อยู่บ้าง ผมว่ามันเป็นกรณีศึกษาที่น่าสนใจ และมันบอกอะไรให้เราได้หลายอย่าง

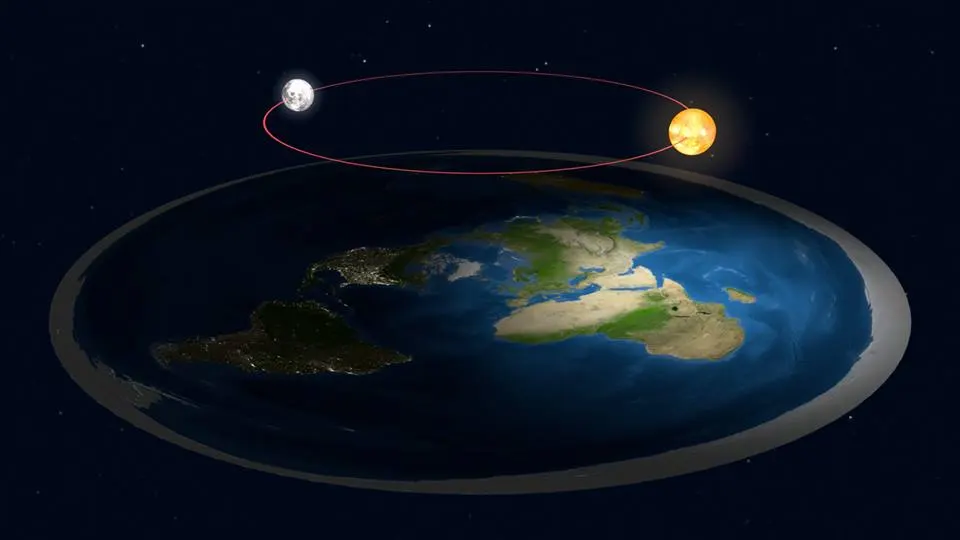
โลกแบนเขาเชื่อว่าโลกแบนเป็นจานกลม โดยมีขั้วโลกเหนืออยู่ตรงกลาง แต่หากดวงอาทิตย์เคลื่อนที่ไปอยู่ใต้จานในเวลากลางคืน เราจะไม่สามารถอธิบายได้ว่าเพราะเหตุใดประเทศสหรัฐกับไทยจึงมีเวลาไม่ตรงกัน พวกโลกแบนก็เลยอธิบายว่าดวงอาทิตย์ลอยอยู่เหนือจานนี้ เคลื่อนที่เป็นวงกลมรอบๆ ขั้วโลก เหนือบริเวณที่เราเรียกว่า "เส้นศูนย์สูตร" ดังภาพ ซึ่งเป็นเหตุผลว่าทำไมเราจึงมี time zone ที่แตกต่างกัน

ปัญหาต่อมาก็คือ ถ้าเป็นเช่นนั้นแล้วดวงอาทิตย์จะลับขอบฟ้าได้อย่างไร โลกแบนจึงอธิบายว่า มันเป็นผลจาก perspective เหมือนกับที่เครื่องบินดูเหมือนเคลื่อนที่ใกล้ขอบฟ้าลงเรื่อยๆ ทั้งๆ ที่มันบินอยู่ความสูงเท่าเดิม

นอกจากนี้ ชาวโลกแบนยังมีคำอธิบายพิศดารกันไปอีกต่างๆ นานา เช่น ซีกโลกใต้ไม่มีจริง ขั้วโลกใต้เป็นเพียงเรื่องหลอกลวง และชาวออสเตรเลียทุกคนเป็นเพียงนักแสดงที่เอาไว้ตบตาผู้คน และทุกๆ ครั้งที่มีคนไปเที่ยว "ออสเตรเลีย" นักบินก็รู้เห็นเป็นใจด้วย และแกล้งบินอ้อมไปจอดที่อื่น ที่จัดฉากว่าเป็นทวีปออสเตรเลีย ฯลฯ

แต่ในที่นี้...เอาเป็นว่าเราจะไม่พูดถึงย่อหน้าสุดท้ายละกัน วันนี้เราจะมาพูดถึงกันแค่ทฤษฎีที่ว่า โลกแบน และดวงอาทิตย์โคจรเป็นวงกลมเหนือแผ่นโลก

หากเราสังเกตดูดีๆ จะพบว่าแนวทางของทฤษฎีโลกแบนเหล่านี้ มีข้อบกพร่องสำคัญอยู่สองอย่าง นั่นก็คือ

1. ปฏิเสธหลักฐานทุกอย่างที่ขัดแย้งกับความเชื่อ
2. ไม่มีความพยายามที่จะอธิบายเชิงคณิตศาสตร์

ซึ่งในทางวิทยาศาตร์แล้วนั้น เมื่อไรก็ตามที่เราพบหลักฐานที่ขัดแย้งกับความเชื่อเดิมของเรา สิ่งที่ต้องผิดไปทันที ก็คือความเชื่อเดิมของเรา (ไม่ใช่หลักฐาน) นักวิทยาศาสตร์ "พร้อมที่จะผิด" ทันทีที่เราค้นพบปรากฏการณ์ที่ขัดแย้งกับทฤษฎีของเรา และด้วยหลักการนี้นั่นเอง ที่นำไปสู่การค้นพบอันยิ่งใหญ่หลายครั้งในประวัติศาสตร์ เช่น การปล่อยลูกเหล็กของกาลิเลโอที่ทำให้เราเข้าใจความเร่งโน้มถ่วง การทดลองของ Louise Pasteur ที่ค้นพบว่าสิ่งมีชีวิตไม่สามารถเกิดขึ้นได้เองได้ ซึ่งนำไปสู่การฆ่าเชื้อในทางการแพทย์ในที่สุด และลดอัตราการตายในรพ. ได้อย่างมาก

แต่อีกข้อที่สำคัญไม่แพ้กันเลย ก็คือ ในวิทยาศาสตร์นั้น เราพยายามอธิบายปรากฏการณ์ทางธรรมชาติ ที่บันทึกเอาไว้ด้วยภาษาของ "คณิตศาสตร์"

นั่นคือ เราไม่ได้ต้องการจะทราบแค่ว่าวัตถุตกลงจากที่สูงลงสู่ที่ต่ำ แต่เราต้องการจะทราบว่า "ด้วยอัตราเร่งเท่าใด" "ด้วยเวลาที่เท่ากันหรือไม่" และเราต้องการจะสร้างแบบจำลองหรือสมการทางคณิตศาสตร์ เพื่อที่เราจะสามารถ "ทำนาย" ได้ว่า ถ้าหากทฤษฎีของเราเป็นจริง เราจะต้องพบว่าค่าที่วัดได้มีปริมาณเท่าใด ซึ่งหากค่าที่วัดได้ต่างออกไปจากคำทำนาย ก็เท่ากับว่าทฤษฎีของเราจำเป็นต้องล้มเลิกไป เช่น เมื่อใดก็ตามที่วัตถุชนกัน ผลคูณของมวลกับความเร็วจะคงที่ เมื่อมีมวลสูญหายไป พลังงานที่ปลดปล่อยออกมาจะเท่ากับ E=mc^2 มวลสองมวลจะมีแรงกระทำเท่ากับ F=GMm/R^2 สิ่งเหล่านี้เรียกว่า testable prediction (คำทำนายที่สามารถตรวจสอบได้)

นักปราชญ์ชาวกรีก Eratosthenes เมื่อ 2,000 กว่าปีที่แล้ว ได้ทราบมาว่า ณ เมือง Syene ในวันครีษมายันของทุกปีเวลาเที่ยงวันดวงอาทิตย์จะอยู่เหนือศีรษะพอดี และสามารถสังเกตเห็นเงาสะท้อนของดวงอาทิตย์ในบ่อน้ำได้ เขาจึงได้ทำการทดลองเดียวกันที่เมือง Alexandria และพบว่าดวงอาทิตย์เที่ยงวันที่เมือง Alexandria นั้นไม่ได้อยู่เหนือศีรษะและเยื้องไปเล็กน้อย แต่หากผู้สังเกตจากทั้งสองตำแหน่งสังเกตดวงอาทิตย์ดวงเดียวกัน นั่นหมายความว่าจะต้องเป็นพื้นโลกใต้พวกเขาต่างหาก ที่ทำมุมไม่เท่ากัน เช่นเดียวกับพื้นผิวของทรงกลม

แต่ Eratosthenes ไม่เพียงแต่บอกว่ามุมไม่เท่ากันเท่านั้น เขายังทำการวัดและพบว่ามุมของดวงอาทิตย์เที่ยงวันในวันครีษมายัน ณ เมือง Alexandria นั้นเบี่ยงออกไป 1/50 ของวงกลม นั่นทำให้เขาสามารถทำนายได้ว่า หากใครสักคนเดินทางไปในทิศทางเดียวกัน เป็นระยะทาง 50 เท่าของระยะทางระหว่าง Syene กับ Alexandria เขาจะต้องกลับมายังจุดเดิม นี่คือ testable prediction ที่ทุกวันนี้เราพบแล้วว่าเป็นไปตามที่ Eratosthenes ทำนายเอาไว้

แต่หากเราไปถามชาวโลกแบนว่า ในแบบจำลองของพวกเขานั้น ดวงอาทิตย์จะมีขนาดใหญ่แค่ไหน อยู่สูงจากแผ่นโลกแค่ไหน และเคลื่อนที่ด้วยอัตราเร็วเท่าใด เราจะไม่พบชาวโลกแบนคนใดที่พร้อมที่จะให้คำตอบได้ เพราะหากเราทราบจำนวนทั้งสามแล้วนั้น เราจะสามารถสร้างคำทำนายและตรวจสอบได้จากการวัดอัตราการเคลื่อนที่และขนาดปรากฏของดวงอาทิตย์จริง และสามารถพบได้ทันทีว่าแบบจำลองนั้นผิดหรือไม่

ซึ่งหากเราย้อนกลับไปดูคำอธิบายที่บอกว่าการตกของดวงอาทิตย์นั้นเป็นผลมาจาก perspective แล้ว เราควรจะทำนายได้ว่าดวงอาทิตย์ควรจะมีขนาดเล็กลงเรื่อยๆ และเคลื่อนที่ด้วยอัตราช้าลงเรื่อยๆ เมื่อเข้าใกล้ขอบฟ้า (เช่นเดียวกับเครื่องบิน) แน่นอนว่าในความเป็นจริงแล้วนั้นดวงอาทิตย์มีขนาดปรากฏคงที่ตลอดทั้งวัน และก็มีอัตราในการเคลื่อนที่ 15 องศาทุกๆ หนึ่งชม. คงที่ตลอด ไม่ว่าจะอยู่ใกล้ขอบฟ้าเพียงใด ซึ่งเท่ากับว่าแบบจำลอง perspective นี้ไม่สามารถอธิบายได้ แต่แบบจำลองที่โลกเป็นทรงกลมหมุนด้วยอัตราเร็วหนึ่งรอบ ทุกๆ 23 ชั่วโมง 56 นาที และโคจรรอบดวงอาทิตย์ปีละ 365 วันนั้น สอดคล้องทุกประการกับอัตราการเคลื่อนที่ของดวงอาทิตย์ที่สังเกตได้

จะสังเกตได้ว่า การอธิบายเชิงปริมาณนั้นเป็นวิธีที่มีประสิทธิภาพเพียงใดในการทดสอบทฤษฎีของเรา และการมองข้ามรายละเอียดทางคณิตศาสตร์ บางครั้งก็อาจทำให้ทฤษฎีที่ควรจะชัดเจนว่าผิด กลับกลายเป็นทฤษฎีที่ฟังดูไม่ได้ถูกไม่ได้ผิดขึ้นมา เพราะเราไม่สามารถตรวจสอบได้

เพราะในวิทยาศาสตร์นั้น เราไม่ได้สนใจเพียงแต่คำถามว่า "อธิบายได้อย่างไร" แต่ทฤษฎีของเราจะต้องสามารถมี testable prediction ที่ทำนายได้ว่า "เท่าไหร่" และเมื่อใดก็ตามที่เราพบว่าการสังเกตนั้นขัดแย้งกับสิ่งที่ทฤษฎีทำนายเอาไว้ ทฤษฎีของเราก็จะเป็นอันต้องถูกล้มล้างไป และเป็นหน้าที่ของเราที่จะต้องคิดค้นทฤษฎีและแบบจำลองทางคณิตศาสตร์ใหม่ขึ้นมาเพื่ออธิบายปรากฏการณ์ที่เราสังเกตเห็น