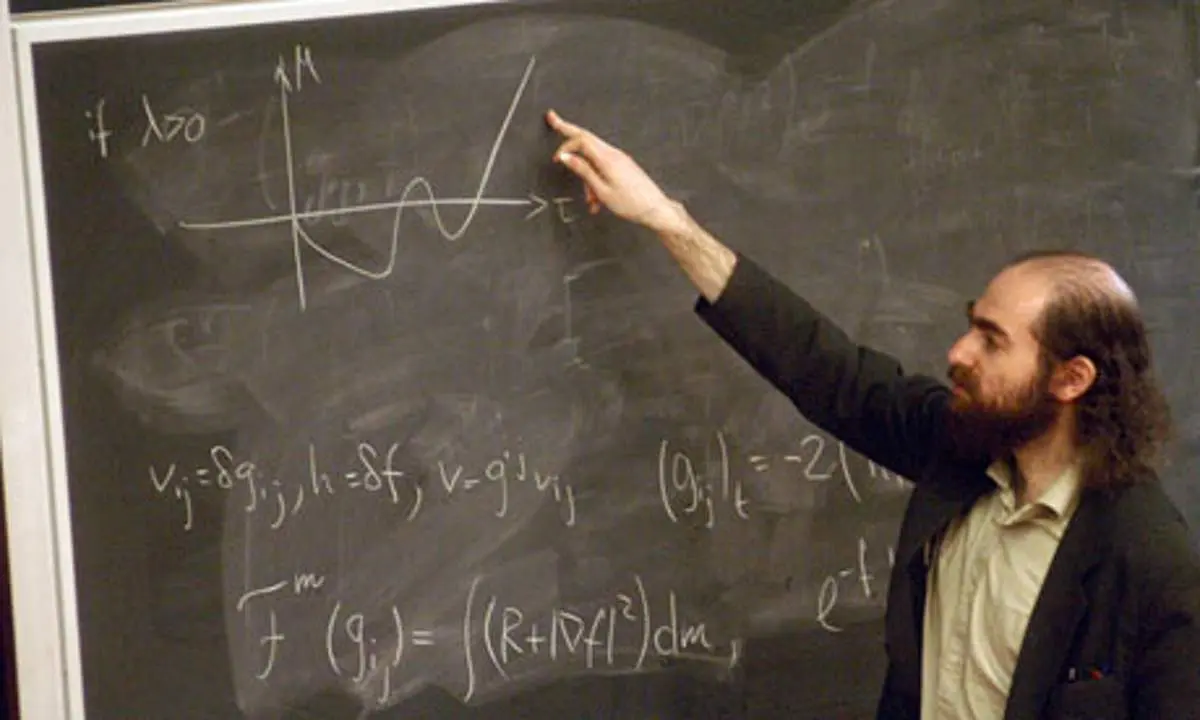โจทย์คณิตศาสตร์ที่ยากที่สุด ที่มนุษย์ยังไม่สามารถหาคำตอบได้
Millennium Prize Problems
หรือ 'ปัญหารางวัลมิลเลนเนียม'
คือชุดของปัญหาทางคณิตศาสตร์ จำนวน 7 ข้อ ที่ยังไขไม่ได้
ซึ่งระบุโดยสถาบันคณิตศาสตร์เคลย์ ในปี 2543 สถาบันประกาศว่า
ใครก็ตามที่แก้ปัญหาเหล่านี้ได้สำเร็จ (เพียงหนึ่งใน 7 ข้อ)
จะได้รับรางวัลเป็นจำนวนเงินหนึ่งล้านดอลลาร์
(ประมาณ 34 ล้านบาท) ปัญหาครอบคลุมด้านต่างๆ ของคณิตศาสตร์
และถือเป็นปัญหาที่ท้าทายและสำคัญที่สุดในสาขานี้
นี่คือคำอธิบายสั้นๆ ของแต่ละปัญหา (ปัญหาในทางคณิตศาสตร์)
การคาดคะเนของ Birch และ Swinnerton-Dyer
(Birch and Swinnerton-Dyer conjecture)
ปัญหานี้เกี่ยวข้องกับเส้นโค้งวงรี ซึ่งเป็นวัตถุทางคณิตศาสตร์ประเภทหนึ่ง
และความเชื่อมโยงกับทฤษฎีจำนวน มันเสนอว่ามีความสัมพันธ์พื้นฐาน
ระหว่างจำนวนจุดตรรกยะบนเส้นโค้งวงรี และคุณสมบัติบางอย่าง
ของฟังก์ชันทางคณิตศาสตร์ที่เกี่ยวข้องกันของเส้นโค้ง
ข้อความคาดการณ์ของฮอดจ์
(Hodge Conjecture)
ปัญหาเกี่ยวข้องกับวัฏจักรเกี่ยวกับพีชคณิต ซึ่งเป็นวัตถุทางเรขาคณิต
ที่กำหนดไว้ในเรขาคณิตเกี่ยวกับพีชคณิต การคาดเดาชี้ให้เห็นว่าวัฏจักรบางประเภท
สามารถแสดงเป็นการรวมกันของวัฏจักรที่ง่ายกว่าได้
ปัญหาการมีอยู่ของนาเวียร์-สโตกส์และความราบเรียบ
(Navier–Stokes existence and smoothness)
ปัญหานี้เกี่ยวข้องกับการเปลี่ยนแปลงของของไหล และพฤติกรรมของการไหลของของไหล
มันพยายามที่จะพิสูจน์ว่าคำตอบของสมการ Navier-Stokes
ซึ่งอธิบายการเคลื่อนที่ของของไหลนั้นมีอยู่จริง และยังคงราบรื่นตลอดเวลาหรือไม่
ปัญหาพีและเอ็นพี
(P versus NP problem)
ปัญหานี้อยู่ในขอบเขตของทฤษฎีความซับซ้อนทางการคำนวณ
ถามว่าทุกปัญหาที่โซลูชันสามารถตรวจสอบได้อย่างมีประสิทธิภาพ
สามารถแก้ไขได้อย่างมีประสิทธิภาพหรือไม่
สมมติฐานรีมันน์
(Riemann hypothesis)
เสนอโดยแบร์นฮาร์ด รีมันน์ ปัญหานี้เกี่ยวข้องกับการกระจายของจำนวนเฉพาะ
มันเกี่ยวข้องกับตำแหน่งของศูนย์ที่ไม่สำคัญของฟังก์ชันซีตาของ Riemann
และแนะนำว่าพวกมันทั้งหมดอยู่บนเส้นเฉพาะในระนาบเชิงซ้อน
ปัญหาการมีอยู่ของทฤษฎีหยาง-มิลส์ และมวลพื้น
(Yang–Mills existence and mass gap)
ปัญหานี้เกี่ยวข้องกับทฤษฎีสนามควอนตัม มีจุดมุ่งหมายเพื่อตรวจสอบว่า
ทฤษฎี Yang-Mills ซึ่งอธิบายพฤติกรรมของอนุภาคมูลฐานมีช่องว่างมวลหรือไม่
(หมายถึงมีความแตกต่างของพลังงานระหว่างสถานะพื้นและสถานะตื่นเต้นต่ำสุด)
ข้อความคาดการณ์ของปวงกาเร
(Poincaré conjecture)
ปัญหานี้เสนอโดย Henri Poincaré เดิมทีเกี่ยวข้องกับรูปร่าง
และโทโพโลยีของปริภูมิสามมิติ
มันถามว่าทุกๆสามมิติที่เชื่อมต่อกันง่ายๆ สามมิติแบบปิดนั้น
เป็นโฮมีโอมอร์ฟิคเป็นสามมิติหรือไม่ (วัตถุทางเรขาคณิตประเภทหนึ่ง)
(Grigori Perelman
คนแรกที่พิสูจน์ 1 ใน 7 ปัญหานี้ได้สำเร็จ)
ปัญหาเหล่านี้ได้รับการพิสูจน์แล้วว่ายากเป็นพิเศษ
และจนถึงตอนนี้ มีเพียงข้อเดียวในนั้น นั่นคือ
'ข้อความคาดการณ์ของปวงกาเร' (Poincaré Conjecture)
ที่ได้รับการพิสูจน์จนสำเร็จ โดย Grigori Perelman นักคณิตศาสตร์ชาวรัสเซีย
ซึ่งได้พิสูจน์สำเร็จในปี 2546 อย่างไรก็ตาม เขาปฏิเสธเงินรางวัลจำนวนนี้
 ฝรั่งย้ายมาอยู่ไทยแต่ไม่ฝันหวาน ชีวิตจริงโคตรเรียล เจ็บจริง เหงาจริง แต่ก็ยังเลือกจะยิ้มอยู่ที่นี่
ฝรั่งย้ายมาอยู่ไทยแต่ไม่ฝันหวาน ชีวิตจริงโคตรเรียล เจ็บจริง เหงาจริง แต่ก็ยังเลือกจะยิ้มอยู่ที่นี่ เราจะไม่ยอมเห็นภาพนี้ คนเดียว ขำๆ กันไป
เราจะไม่ยอมเห็นภาพนี้ คนเดียว ขำๆ กันไป รวมภาพเรียกรอยยิ้มประจำวันนี้ 11/04/68 ใกล้วันสงกรานต์แล้ว วันนี้หลายๆคนเลิกงานแล้วคงออกเดินทางท่องเที่ยวกันแล้วซิน๊า
รวมภาพเรียกรอยยิ้มประจำวันนี้ 11/04/68 ใกล้วันสงกรานต์แล้ว วันนี้หลายๆคนเลิกงานแล้วคงออกเดินทางท่องเที่ยวกันแล้วซิน๊า เพจดัง โพสต์เทียบ ตึกถล่ม 2 ภาพ เห็นแล้วอึ้ง ตึกผงปูน สตง. ไม่ได้มาตรฐาน
เพจดัง โพสต์เทียบ ตึกถล่ม 2 ภาพ เห็นแล้วอึ้ง ตึกผงปูน สตง. ไม่ได้มาตรฐาน ไม่ขอใช้สักบาท! สไปร์ท SPD เปิดยอดรายได้คลิปดราม่า พร้อมขอโทษสังคม
ไม่ขอใช้สักบาท! สไปร์ท SPD เปิดยอดรายได้คลิปดราม่า พร้อมขอโทษสังคม เตือนภัย "ปากกาเมจิก" ซึมถุงอาหาร
เตือนภัย "ปากกาเมจิก" ซึมถุงอาหาร ทำเกินเบอร์! คู่รักดาราเล่นใหญ่ เซิร์ฟดินสอพองจัดเต็มไม่ห่วงหล่อสวย
ทำเกินเบอร์! คู่รักดาราเล่นใหญ่ เซิร์ฟดินสอพองจัดเต็มไม่ห่วงหล่อสวย พบทองคำหนักเกือบ 18 กิโลกรัม ในบ่อน้ำลึก
พบทองคำหนักเกือบ 18 กิโลกรัม ในบ่อน้ำลึก สงกรานต์เวอร์ชั่นเขมร เล่นน้ำก่อนไทย แถมเปิดเพลงไทยอีกต่างหาก แบบนี้เรียกว่าร่วมฉลองหรือแอบเคลม
สงกรานต์เวอร์ชั่นเขมร เล่นน้ำก่อนไทย แถมเปิดเพลงไทยอีกต่างหาก แบบนี้เรียกว่าร่วมฉลองหรือแอบเคลม ลัคกี้ แมวหน้าเคลิ้มที่โด่งดังในอินเตอร์เน็ต
ลัคกี้ แมวหน้าเคลิ้มที่โด่งดังในอินเตอร์เน็ต คนละเรื่อง?? กรณี สส. อภิปรายโยง จันทรุปราคา-สุริยุปราคา , พายุสุริยะ และวงแหวนดาวเสาร์ เข้ากับการเกิดแผ่นดินไหว
คนละเรื่อง?? กรณี สส. อภิปรายโยง จันทรุปราคา-สุริยุปราคา , พายุสุริยะ และวงแหวนดาวเสาร์ เข้ากับการเกิดแผ่นดินไหว แม่พระตัวจริง! อั้ม พัชราภา เนรมิตคฤหาสน์ให้น้องหมา ใหญ่จนแฟนๆ ตะลึง
แม่พระตัวจริง! อั้ม พัชราภา เนรมิตคฤหาสน์ให้น้องหมา ใหญ่จนแฟนๆ ตะลึง เพื่อนเมียแฉ "ไฮโซเก๊" ถามหน่อยคนรวยที่ไหนใส่รองเท้าส้นถาก!?
เพื่อนเมียแฉ "ไฮโซเก๊" ถามหน่อยคนรวยที่ไหนใส่รองเท้าส้นถาก!? จีนเรียกร้องไม่ให้พลเมือง เข้าร่วมสงคราม หลังทหารจีนถูกจับในยูเครน
จีนเรียกร้องไม่ให้พลเมือง เข้าร่วมสงคราม หลังทหารจีนถูกจับในยูเครน คนละเรื่อง?? กรณี สส. อภิปรายโยง จันทรุปราคา-สุริยุปราคา , พายุสุริยะ และวงแหวนดาวเสาร์ เข้ากับการเกิดแผ่นดินไหว
คนละเรื่อง?? กรณี สส. อภิปรายโยง จันทรุปราคา-สุริยุปราคา , พายุสุริยะ และวงแหวนดาวเสาร์ เข้ากับการเกิดแผ่นดินไหว ลัคกี้ แมวหน้าเคลิ้มที่โด่งดังในอินเตอร์เน็ต
ลัคกี้ แมวหน้าเคลิ้มที่โด่งดังในอินเตอร์เน็ต